|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Brand group - Coherent Quantum Gases
The coherent quantum gases group is interested in various aspects of
the physics of ultracold atomic gases. Of particular interest are
nonlinear wave phenomena (solitons) and strong correlations in the Bose and Fermi quantum gases.
Principal Investigator: Prof. Joachim Brand
Funding success - We are hiring!
The grants just keep on rolling in. See jobs!
-
The Marsden project Three atoms in a tight spot was selected for funding by the Royal Society of New Zealand. The project will run from 2021 to 2024.
-
DWC 2.0: The Dodd-Walls Centre for Photonic and Quantum Technologies was refunded for its second term from 2021 through to 2028. We are part of the research question "Quantum and Classical Emulation".
From left to right: Ray (Mingrui) Yang, Dr. Christopher Bradly, Prof. Joachim Brand, Matija Čufar, Sarthak Choudhury
Previous group members
Dr. Ulrich Ebling
Dr. Jan Major
Steven van Ommen
Dr. Péter Jeszenszki
Dr. Sophie Shamailov
Dr. Jayson Cosme
Dr. Oleksandr Fialko
Adrien Didier
Dr. Lauri Toikka
Dr. Shreyoshi Gosh
Dr. Antonio Muñoz Mateo
Alex Ayet
Dr. Alberto Cetoli
Gabriele Jaritz
Dr. Renyan Liao
Dr. Thomas Ernst
Dr. David Hallwood
Jake Gulliksen
Marie-Coralie Delattre
|
Musical vibration patterns inspire the search for defects in ultra-cold atomic gase
Similar to musical instruments, superfluid defects can resonate at characteristic frequencies that produce intriguing patterns.
The explanation of this phenomenon goes back to the eighteenth century, when Ernst Chladni observed grains of sand assemble in geometric patterns on the surface of a plate excited to characteristic tones with a bow. The lines of sand that we nowadays call Chladni figures trace the nodal lines of vibration modes. In a similar fashion to Chladni`s plates, a standing wave in a confined superfluid called dark soliton possesses characteristic vibration modes with geometric patterns of nodal lines. Being unstable vibrations, the dark soliton decays leaving behind a skeleton of vortex lines that make up solitary waves themselves. The two simplest structures, a single vortex line called solitonic vortex, and a vortex ring have already been observed in quantum gases. However, solitonic vortices and vortex rings are just two members of a whole family of standing waves, the Chladni solitons.
Stability and dispersion relations of three-dimensional solitary waves in trapped Bose-Einstein condensates
A. Muñoz Mateo, J. Brand
New J. Phys. 17, 125013 (2015)
Chladni solitons and the onset of the snaking instability for dark solitons in confined superfluids
A. Muñoz Mateo, J. Brand
Phys. Rev. Lett. 113, 255302 (2014)
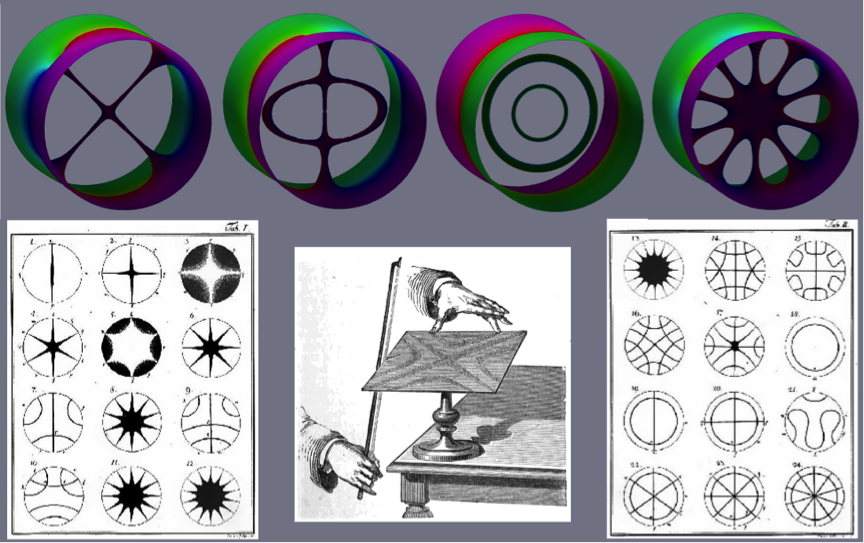
Chladni solitons made of vortex lines in a superfluid (above) versus Chladni figures made of nodal lines of plate vibrations (below). Central image from William Henry Stone, Elementary Lessons on Sound (Macmillan and Co., London, 1879), p. 26, fig. 12; and side images from Chladni, E. F. F., Entdeckungen ueber die Theorie des Klanges (Weidmanns Erben und Reich, 1787).
|
Research topics
Solitons in Bose-Einstein Condensates
Particle and Wave Nature of Matter-Wave Bright Solitons
Bose-Einstein condensate with attractive interactions can form
non-spreading wavepackts, a sort of self-cohesive drops also called bright solitons. Being a special
sort of nonlinear waves, bright solitons share many properties of
classical particles. However, depending on the circumstances they may
still reveal their quantum nature. Read more about ...
Soliton and vortex ring ring collisions
|
Solitons and vortex rings are examples of nonlinear wave phenomena, which
maintain their shape during propagation. The collisions of such waves were recently observed in a Bose-Einstein
condensate for the first time. The experiment at Harvard University showed
evidence of unexpected shell-like structures. Simulations give evidence that
these structures are hybride objects composed of soliton fronts and vortex
rings.
-
Phys. Rev. Lett. 95, 110401 (2005)
-
Phys. Rev. Lett. 94, 040403 (2005)
Story on Physics News Update
Article for Physik in unserer Zeit
|

|
Solitonic vortices and the snake instability
|
What happens to vortices when they are put into a narrow channel? What is the
1D analog of a vortex? We study the effects of transverse confinement on vortices in a repulsive,
elongated BEC. In a regime where the width of the elongated trap is about 6 to
12 healing lengths, vortices show properties usually associated with solitons.
In particular, their velocity may be associated with a characteristic phase
step and collision properties are soliton-like. Thus we speak of solitonic
vortices. A connection can be made to the snake instability of soliton stripes
which is also a mechanism that may be exploited to experimentally create
solitonic vortices [1 ].
A different way of producing solitonic vortices in a controlled manner is
stirring in a toroidal trap [2 ].
Properties are studied using 2 and 3D simulations of the Gross-Pitaevskii
equation but also using the method of image charges which yields an exactly
solvable model of vortex dynamics.
[1] Phys. Rev. A 65 (2002)
04361
[2]J. Phys. B: At. Mol. Opt. Phys. 34
(2001) L113-L119
|

|
Strongly-Interacting Quantum Gases
We are interested in the many-body theory of quantum gases under the
influence of strong correlations. In particular there are interesting
crossover scenarios for a Bose gas in one dimension or a two-component
Fermi gas under the influence of a Feshbach resonance.
Is the 1D Bose gas superfluid?
The 1D Bose gas at zero temperature has many surprising properties that are
very distinct from 3D Bose-Einstein condensates including the loss of phase
coherence and a fermionic excitation spectrum with appearance of two branches
of elementary excitations. According to the Landau criterion of superfluidity
this should prevent the possibility of superfluidity. However, according to
common definitions of condensed-matter physics, the superfluid fraction of the
interacting 1D Bose is known to be 100%. In order to really understand the
superfluid properties of the 1D Bose gas we calculate the dynamic structure
factor and the drag force that a heavy but small particle feels when dragged
through the gas. Check back on this page to read our upcoming preprint when it
is ready or read our previous papers on the 1D Bose gas:
Phys. Rev. A 73, 023612 (2006)
Phys. Rev. A. 72, 033619 (2005)
Phys. Rev. A. 70, 043622 (2004)
J. Phys. B: At. Mol. Opt. Phys. 37 (2004) S287-S300
Levinson's theorem for atomic scattering on Bose-Einstein condensates
Levinson's theorem of potential scattering connects the number of bound
states of a given potential to the phase shifts of scattering solutions.
Excitations of a weakly interacting Bose condensate are described by the
coupled Bogoliubov equations. Scattering solutions for a finite trapping
potential describe the scattering of single, identical particles. Can
Levinson's theorem be generalized and the number of bound collective
excitations of a condensate be linked with the phase shifts of single-particle
scattering? Particularly interesting situations occur for kinks or vortices in
shallow traps as they can give rise to 'bound states in the continuum' of
single particle scattering.
Phys. Rev. Lett. 91, 070403 (2003)
Software
- Rimu.jl : Random integrators for quantum many-body systems. Projector quantum Monte Carlo based on full configuration interaction quantum Monte Carlo (FCIQMC)
- QiwiB: Implementation of multi-configurational time-dependent Hartree for bosons (MCTDHB)
Links



Maintained by Peter Schwerdtfeger | Last updated: June 2019 | Copyright 2014 | Massey University
|
|



